(Difference between revisions)
| Revision as of 13:33, 8 September 2006 Peter (Talk | contribs) ← Previous diff |
Revision as of 11:52, 15 September 2006 Peter (Talk | contribs) (→Calibrating Yield) Next diff → |
||
| Line 3: | Line 3: | ||
| ==Calibrating Yield== | ==Calibrating Yield== | ||
| - | The yield function is a statistically derived function relating the water balance parameters (which constitute the outputs of the "agmet model") and the other factors (farm inputs, trend) or NDVI with station yield. | + | The yield function is a statistically derived function relating the water balance parameters (which constitute the outputs of the water balance model) and the other factors (farm inputs, trend) or NDVI with station yield. Once this function has been established, it can be used for early crop yield forecasting. |
| - | The yield function is valid for a crop and a group of stations in an homogeneous cropping area. The input data correspond to different geographical units, from weather stations, to pixels (NDVI, CCD: 50 km2) to administrative units. It is an important step in the forecasting method to convert the data to comparable units (area averaging), usually administrative areas that are used by planners or decision makers in the field of food security. | + | Although many different equations are possible, the most widely used one is the outcome of a multiple linear regression procedure: |
| + | <blockquote> | ||
| + | Y = a + b1X1 + b2X2 + b3X3 | ||
| + | </blockquote> | ||
| + | |||
| + | where b1 to b3 are the corresponding X coefficients. | ||
| Line 14: | Line 19: | ||
| - | Regression lines similar to the one above have been used to prepare the yield maps shown in the following Outputs section | + | |
| + | |||
| + | |||
| + | |||
| </Blockquote> | </Blockquote> | ||
Revision as of 11:52, 15 September 2006
Calibrating Yield
The yield function is a statistically derived function relating the water balance parameters (which constitute the outputs of the water balance model) and the other factors (farm inputs, trend) or NDVI with station yield. Once this function has been established, it can be used for early crop yield forecasting.
Although many different equations are possible, the most widely used one is the outcome of a multiple linear regression procedure:
Y = a + b1X1 + b2X2 + b3X3where b1 to b3 are the corresponding X coefficients.
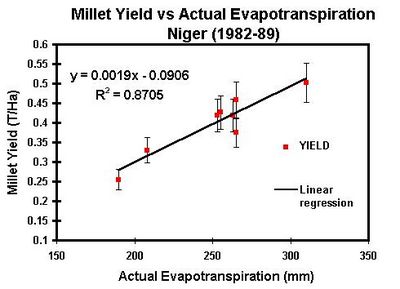
Besides is a very simple example of a yield function in an area where yields are mainly conditioned by limited water supply, as is the case -by definition- in most semi-arid areas of the world.