Revision as of 12:34, 24 August 2006; view current revision
←Older revision | Newer revision→
By R. Gommes
Analyzing yield trends
An increase in crop yield from year to year may be explained by gradual improvements in technology, while other variables such as weather conditions, pests and diseases, input availability are all fairly constant or “under control”. The factors which affect the variability of agricultural yields can roughly be grouped in three categories according to their variations over time:
- growing smoothly, such as more or less regular technology and management trends (i.e. mechanization, varieties, irrigation, and the farmers know-how), but growing more abruptly for several years in succession in the case of innovations. A typical innovation would be the new introduction of irrigation;
- discontinuous, like extreme factors of various origins and policy decisions which affect management (for instance, farmers may decide to use less fertilizer if it is no longer subsidized) or infrastructure, such as the construction of a road which provides access to new markets;
- pseudo-cyclic, like weather. The result may be a complex curve where it is often rather difficult to separate weather from other factors, particularly if weather itself is affected by a trend...
A graphical example is given below.
A theoretical example of some of the factors affecting agricultural yields (the heavy red line): technology and management trends, innovation, policy, extreme factors and weather 
Detrending yield
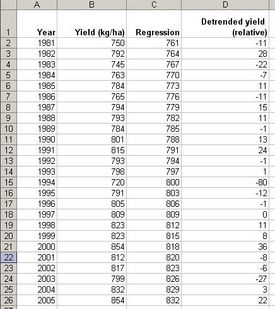
Getting a good series of yield data requires the application of some detrending statistics to get the so-called detrended yield.
The detrended yield is the departure of yield values from the time-trend, assumed to take into account the technology and management component of yield. The time-trend accounts for about 80% of the total variation of yields, leaving about 20% to be accounted for by other factors.
Detrending yield requires two steps. The first step involves the fitting of a smooth curve through the yield statistics. In a second step the actual detrended yield is calculated. An example in Excel is given below.
Suppose the following yield statistics from 1981 to 2005 for an imaginary place. When a linear regression is applied, the slope and intercept at the bottom are calculated. This leads to a “predicted” normal yield in the third column. 
The detrended relative yield can be added by subtracting the second and third column. 
